-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
MX2 Marathon (4 Viewers)
- Thread starter dan964
- Start date
pikachu975
Premium Member
Re: HSC 2018 MX2 Marathon
(x+2i)^2 = x^2 + 4xi - 4
Since it is real then Im(z^2) = 0
so 4x = 0
x = 0
Hence z = 2i
So let z = x + 2i
(x+2i)^2 = x^2 + 4xi - 4
Since it is real then Im(z^2) = 0
so 4x = 0
x = 0
Hence z = 2i
Re: HSC 2018 MX2 Marathon
I cant get the answer.. the answer is +- (2+i)
how about if re(z) is 2Im(z) and z^2-4i is real
I cant get the answer.. the answer is +- (2+i)
Last edited:
Paradoxica
-insert title here-
Re: HSC 2018 MX2 Marathon
Prove the ellipses:
^2}{a^2} + \frac{y^2}{b^2} = 1, \frac{x^2}{a^2} + \frac{(kx + y)^2}{b^2} = 1)
where k is an arbitrary real number
have the same area as the ellipse
Prove the ellipses:
where k is an arbitrary real number
have the same area as the ellipse
Last edited:
Re: HSC 2018 MX2 Marathon
^2}{p^2} + \frac{(cx + dy)^2}{q^2} = 1)
has area
Continuing on, prove that the area of the ellipse defined byProve the ellipses:
have the same area as the ellipse
has area
Paradoxica
-insert title here-
Re: HSC 2018 MX2 Marathon
Letting the value of the solution to x = cos(x) be r, the following area expressions are obtained through integration:
A₁ = sin(r) - r²/2
A₂ = 1 - sin(r) + r²/2
A₂ - A₁ = 1 - 2sin(r) + r²
r > sin(r) (proof is trivial and left as an exercise)
- 2sin(r) > - 2r
1 - 2sin(r) + r² > 1 - 2r + r² = (1-r)² > 0
A₂ - A₁ > 0
A₂ > A₁
Letting the value of the solution to x = cos(x) be r, the following area expressions are obtained through integration:
A₁ = sin(r) - r²/2
A₂ = 1 - sin(r) + r²/2
A₂ - A₁ = 1 - 2sin(r) + r²
r > sin(r) (proof is trivial and left as an exercise)
- 2sin(r) > - 2r
1 - 2sin(r) + r² > 1 - 2r + r² = (1-r)² > 0
A₂ - A₁ > 0
A₂ > A₁
sida1049
Well-Known Member
- Joined
- Jun 18, 2013
- Messages
- 926
- Gender
- Male
- HSC
- 2015
Re: HSC 2018 MX2 Marathon
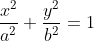
Change to polar form, apply de Moivre's theorem, done. For all of them.
pikachu975
Premium Member
Re: HSC 2018 MX2 Marathon
Realise the denominator and use De Moivre's at the end to get the n in 2ntheta
CapitalSwine
New Member
- Joined
- Jul 12, 2017
- Messages
- 8
- Gender
- Male
- HSC
- 2018
Re: HSC 2018 MX2 Marathon
Appreciate some help with this: Find the range of values of |z| and arg(z) for |z-4-4i|=2sqrt(2)
Appreciate some help with this: Find the range of values of |z| and arg(z) for |z-4-4i|=2sqrt(2)
Re: HSC 2018 MX2 Marathon
Sketch the locus of z and note that the modulus and argument of z use the join of the origin to a point on the circle.
CapitalSwine
New Member
- Joined
- Jul 12, 2017
- Messages
- 8
- Gender
- Male
- HSC
- 2018
Re: HSC 2018 MX2 Marathon
Sent from my Redmi Note 4 using Tapatalk
What is the modulus and argument of z in this case? I got an answer that was different to the one in the textbook.
Sent from my Redmi Note 4 using Tapatalk
altSwift
Member
- Joined
- Jan 6, 2017
- Messages
- 65
- Gender
- Male
- HSC
- 2018
Re: HSC 2018 MX2 Marathon
Find an expression for cos^4x in terms of cos4x and cos2x
Edit: The question is from terry lee so I'm guessing it implies that you use 4U complex techniques rather than 3U, I'm not sure if you can even use 3U for this...
Find an expression for cos^4x in terms of cos4x and cos2x
Edit: The question is from terry lee so I'm guessing it implies that you use 4U complex techniques rather than 3U, I'm not sure if you can even use 3U for this...