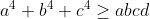Part c will be a walk in the inequalities forest. Are you ready for that? So the first step will be to start with
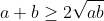
and
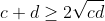
.
Next, we will have to start with the fact that
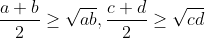
.
There we divide by 2 and using the inequalities that are known we will have
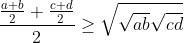
Noting that
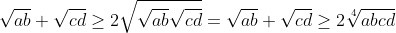
At this momwnt our goal will be to multiply by 2 and then multiply by 2 and in doing so we actually multiply by 4. There you will have
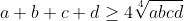
.
Now the question starts.
Do you recall that
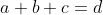
Well, on the LHS of the inequality it will become
\geq{4\sqrt[4]{abcd}})
There,
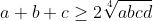
.
I imagine what happens is that out of the rabbit's hat
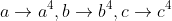
and in doing so it will give us
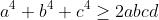
. I assume that
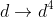
out of nowhere. I could sense that either this is a typo or something shady is happening. If it is the latter please show us.
Thus, we have proven that
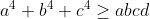
and
.
.
.
.
and in doing so it will give us
. I assume that
out of nowhere. I could sense that either this is a typo or something shady is happening. If it is the latter please show us.