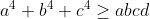mmmmmmmmaaaaaaa
Well-Known Member
- Joined
- Jun 11, 2021
- Messages
- 1,412
- Gender
- Male
- HSC
- 2022
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
No, because if you do that you will have both sides being equal which is no longer an inequality.For part b, not sure, but you could do a = b = c and then sub it in - Could someone verify!
For part b I have an antidote. Do you notice how part b started with "Hence ... "I completed part a
a) a^4+b^4 ≥ 2a^2b^2 etc.
for part b though, I'm unsure what it would be following the same logic
View attachment 34637
Thanks!Part c will be a walk in the inequalities forest. Are you ready for that? So the first step will be to start withand
.
Next, we will have to start with the fact that.
There we divide by 2 and using the inequalities that are known we will have
Noting that
At this momwnt our goal will be to multiply by 2 and then multiply by 2 and in doing so we actually multiply by 4. There you will have
.
Now the question starts.
Do you recall that
Well, on the LHS of the inequality it will become
There,.
I imagine what happens is that out of the rabbit's hatand in doing so it will give us
. I assume that
out of nowhere. I could sense that either this is a typo or something shady is happening. If it is the latter please show us.
Thus, we have proven that