Given a polynomial equation and one or two roots, how does one successfully find the other two or three roots? (depending on either a cubic or quartic equation). I always end up with irrational roots when the question clearly says integer roots. What is the best way to solve an equation using sum and product of roots?
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Polynomial Theory Of Roots (1 Viewer)
- Thread starter ADrew
- Start date
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 877
- Gender
- Male
- HSC
- 2010
an example plz?
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 877
- Gender
- Male
- HSC
- 2010
generally you can just write down all the sums of roots 1/2/3/... at a time
then solve these equations
then solve these equations
@ADrew has posed a very open-ended question that we encounter from time to time on BOS. Such questions are not going to be very helpful to him/her. As Mr Tomato has suggested, best is to pose a specific question. Then one could follow up with a variety of like questions. That way you help yourself greatly.
Last edited:
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 877
- Gender
- Male
- HSC
- 2010
Dear Dr Drongoski@ADrew has posed a very open-ended question that we encounter from time to time on BOS. Such quetions are not going to be very helpful to him/her. As Mr Tomato has suggested, best is to pose a specific question. Then one could follow up with a variety of like questions. That way you help yourself greatly.
Plz call me "funny" if you cbb typing "funnytomato".
Yours, sincerely
Mr Howard Wolowitz Tomato
Okay having trouble with this Q:
New senior maths 3 unit exercise 27 d Q 17:
"Solve the equation 6x^4-11x^3-26x^2+22x+24=0 given that the product of two roots is equal to the product of the other two"
New senior maths 3 unit exercise 27 d Q 17:
"Solve the equation 6x^4-11x^3-26x^2+22x+24=0 given that the product of two roots is equal to the product of the other two"
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Is this what you mean?
Example.
Suppose we have with a zero of -2, find the other zeros.
with a zero of -2, find the other zeros.
Note: We have a polynomial in the form of
Let the zeros be ,
, 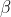 ,
, 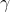
Now,


But we know what one zero is,


Now,


We know that one zero is -2,
= -4)

We now have two equations.
1.
2.
We can rearrange equation 1,

Putting it into equation 2,
 = 2)


(\alpha - 4) = 0)

Example.
Suppose we have
Note: We have a polynomial in the form of
Let the zeros be
Now,
But we know what one zero is,
Now,
We know that one zero is -2,
We now have two equations.
1.
2.
We can rearrange equation 1,
Putting it into equation 2,
kooliskool
Member
- Joined
- Nov 23, 2006
- Messages
- 137
- Gender
- Male
- HSC
- 2007
I agree with Drongoski, it's better to solve for the roots that you can first with substitution, then use what the question gives you to solve for the rest is the best way to do it.
Otherwise it's just algebra bashing the polynomial question if your substitution won't give you any rational roots. (By doing sum 1/2/3/4 at a time, get the simultaneous equations)
Otherwise it's just algebra bashing the polynomial question if your substitution won't give you any rational roots. (By doing sum 1/2/3/4 at a time, get the simultaneous equations)
I found trying to solve the 4 eqns of roots, as apparently intended by the question, difficult. Maybe some of you are better at it. But from the 4 eqns you can derive the result:  . I could and should have used this fact to derive the 2nd root -3/2 from 4/3 - but I completely overlooked this and wasted a lot of time looking for the 2nd root by trial-and-error.
. I could and should have used this fact to derive the 2nd root -3/2 from 4/3 - but I completely overlooked this and wasted a lot of time looking for the 2nd root by trial-and-error.
Last edited:
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 877
- Gender
- Male
- HSC
- 2010
is 4/3 from trial and error?I found trying to solve the 4 eqns of roots, as apparently intended by the question, difficult. Maybe some of you are better at it. But from the 4 eqns you can derive the result:. I could and should have used this fact to derive the 2nd root -3/2 from 4/3 - but I completely overlooked this and wasted a lot of time looking for the 2nd root by trial-and-error.
cos using
Yes - 4/3 came from trial-&-error.
The factors of 24 are 1,2,3,4,6,8,12,24 and of 6 are 1,2,3,6
So potentially, if a rational root exists, it is of form: p/q with p a factor of 24 and q a factor 0f 6. So potentially there are
2 x 8 x 4 = 64 different possibilities, viz:

Because of duplications you end up with around 30 candidates. You plug them into the polynomials and hope you get a zero. Because of the 6 maybe you can try those involving q= 3 earlier. All in all a tedious process unless you have a special calculator with the polynomial P(x) or a simple computer program into which you feed the various candidates and pray for a zero.
Note you can't get the irrational roots this way - or at least I don't know how.
The factors of 24 are 1,2,3,4,6,8,12,24 and of 6 are 1,2,3,6
So potentially, if a rational root exists, it is of form: p/q with p a factor of 24 and q a factor 0f 6. So potentially there are
2 x 8 x 4 = 64 different possibilities, viz:
Because of duplications you end up with around 30 candidates. You plug them into the polynomials and hope you get a zero. Because of the 6 maybe you can try those involving q= 3 earlier. All in all a tedious process unless you have a special calculator with the polynomial P(x) or a simple computer program into which you feed the various candidates and pray for a zero.
Note you can't get the irrational roots this way - or at least I don't know how.
Last edited:

