cssftw
Member
- Joined
- Jun 19, 2009
- Messages
- 207
- Gender
- Male
- HSC
- 2011
So i didn't have much experience with inequality induction, I'd like to know what mark/3 I'd get, probs either 1 or 2/3.
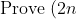!\: \geq \: 2^{n}(n!)^2\\\\\textup{Test for n=1}\\\\\therefore \: \textup{LHS}=(2\times 1)!=2\\\\\textup{RHS}=2^{1}(1!)^2=2\\\\\therefore \textup{LHS}\geq \textup{RHS}\\\\\therefore \textup{True for n=1}\\\\\textup{Assume true for n=k, k integer}\\\\\therefore (2k)!\geq 2^{k}(k!)^2\\\\\textup{Prove for n=k+1}\\\\\therefore (2(k+1))!\\\\=(2k+2)!\\\\=(2k+2)(2k+1)(2k!)\\\\\geq (2k+2)(2k+1)(2^{k}(k!)^2)\\\\=2(k+1)(2k+1)(2^{k}(k!)(k!))\\\\=(2^{k+1})((k+1)!)(2k+1)(k!) ->\textup{It was here I had no idea what to do next - btw note the equal sign instead of the 'greater' sign}\\\\=2^{k+1}[(k+1)!]^2 --> \textup{not too sure if I included this step (might have left it out)}\\\\\therefore \textup{true for n=k+1}\\\\\therefore \textup{true for n=1, true for n=k+1 when true for n=k, k integer}\\\\\therefore \textup{true for n=2, n=3.... true for all positive integers n})
Obviously I didn't know that 2k+1 > k+1 LOL
So is this 1/3 or 2/3? --> let's say I did forget to put in that final step of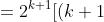!]^2 )
and just went on from the previous step straight to the conclusion -- 1/3 or 2/3?
thanks
Obviously I didn't know that 2k+1 > k+1 LOL
So is this 1/3 or 2/3? --> let's say I did forget to put in that final step of
thanks
Last edited: