Yup what TheOnePheeph said.
Reverse quotient rule is a dodgy inspection method of getting the answer. I'll explain
So we have
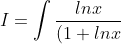^2}dx)
Observe that the denominator is of the form (something)^2. The only way we can get this is when you differentiate something of the form u/v. As this will give you
 = \dfrac{vu' - uv'}{v^2}\hspace{2mm}\text{(Standard Quotient rule)})
Notice the denominator is of the form (something)^2.
We can therefore say the Anti derivative takes the form of
}{1 + lnx})
Now comes the dodgy part. You guess the numerator. Usually it's something simple and you should guess it as something that is similar to the integral. For example if the integral contained a bunch of sines and coses, you might guess sin(x) as the numerator.
If you test 1 and -1 it doesn't work but if you test x which is the second most simplest thing it checks out
And no this isn't taught in the syllabus. This is just intuition you develop over time or by a tutor or someone telling you

