Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Zeta (2) Function (1 Viewer)
- Thread starter U MAD BRO
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
I would say that the original proof (Euler) using the Taylor Series for the Sine function and equating coefficients is the shortest.What is the shortest way to prove thefunction because the one where you use sinx < x < tanx is really really long, elementary but tedious
Is the proof using Fourier series the shortest one?
and why does=
?!?!?
Also, you already have a copy of the proof for that indefinite integral. You use Integration by Parts and the integral reduces to an infinite series, namely zeta_2.
Yes, the Euler proof looks both short and simple.I would say that the original proof (Euler) using the Taylor Series for the Sine function and equating coefficients is the shortest.
Also, you already have a copy of the proof for that indefinite integral. You use Integration by Parts and the integral reduces to an infinite series, namely zeta_2.
Do you use integration by parts to evaluate that integral? Is the working out simple for that integral?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Oh found a little typo, but nothing that will entirely change the proof.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Also in the proof above, I took it for granted that:
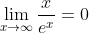
By dominance of functions, but it really should be properly proven (fairly straightforward).
By dominance of functions, but it really should be properly proven (fairly straightforward).
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
L'Hopital's rule ftwAlso in the proof above, I took it for granted that:
But the proof is fairly straightforward. Give it a try yourself you're not convinced =)
Since trials are over, I'll spend my time doing extra curricular stuff, they are so much fun =)Oh found a little typo, but nothing that will entirely change the proof.
and I used this http://mathim.com/Mathstuff a guy taught me how to do do contour integration there ^_^
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
It's good to know this extra stuff because it's interesting, but it's probably best if you focus on the HSC for the moment. You have plenty of time for extra reading afterwards.Since trials are over, I'll spend my time doing extra curricular stuff, they are so much fun =)
and I used this http://mathim.com/Mathstuff a guy taught me how to do do contour integration there ^_^
Yes, you're right, but I'll take a break for a week after trials doing extra curricular stuff, and going to the gym, should be a nice break from studying.It's good to know this extra stuff because it's interesting, but it's probably best if you focus on the HSC for the moment. You have plenty of time for extra reading afterwards.
Then I'll get back to doing past papers all day =)
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Yep I would have done a proper proof using the Taylor Series too, but I would probably also specify for large x and for all n>0 since x^n can be more powerful than e^x within a fairly large domain, given n is large enough.
Riproot
Addiction Psychiatrist
- Joined
- Nov 10, 2009
- Messages
- 8,226
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2017
^Advertising competitors.
Stop annoying me or I'll report you.^Advertising competitors.
lolcakes52
Member
- Joined
- Oct 31, 2011
- Messages
- 283
- Gender
- Undisclosed
- HSC
- 2012
God I love taylor series. When I see a HSC question which uses the first few terms of sin(x) and Newton's method I'm like I SEE WHAT YOU DID THAR!
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
Don't you mean e^x > 1+x+x^2/2 lol?YES! And when it's like e^x < 1+x+x^2/2
But no one at my school has such an appreciation
Yeah, it should be.Don't you mean e^x > 1+x+x^2/2 lol?
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Oh yes, sorry lol
Edit: Actually the question in my trial asked for fx= x-ln(1+x+x^2/2) and it was defined for x<0. It was a calculus inequality with stationary points etc and it ended up being e^x<1+x+x^2/2 for x<0. But for positive x, e^x > 1+x+x^2/2, yes.
Edit: Actually the question in my trial asked for fx= x-ln(1+x+x^2/2) and it was defined for x<0. It was a calculus inequality with stationary points etc and it ended up being e^x<1+x+x^2/2 for x<0. But for positive x, e^x > 1+x+x^2/2, yes.
Last edited:







