Integration Applicaiton (1 Viewer)

[xwrathbringerx]

Show, by integration, that the area of a unit square is divided into four equal parts by the curves y = x^3, y = sqrt(x) and y = x.

Could someone please show me how to set this proof out correctly?

 

[Timothy.Siu]

You could draw it out (to visualise).
Then, just integrate the curves.

The area of the unit square would be 1.
Then, rootx should be 3/4
then, x should be 1/2
and finally x^3 should be 1/4

then you can sorta says its equal.

 

[Drongoski]

Show, by integration, that the area of a unit square is divided into four equal parts by the curves y = x^3, y = sqrt(x) and y = x.

Could someone please show me how to set this proof out correctly?

That's interesting; never knew the said curves partition the unit square into 4 equal parts.

Say the 4 parts are:

A1 = area between y = 1 and y = sqrt(x):
integrating (1 - sqrt(x) ) wrt x between x= 0 to 1, I got 1/3

A2 = area between y = sqrt(x) and y = x
integrating (sqrt(x) - x) the same way: I got 1/6

A3 = area between y = x and y = x³
integrating same way: I got 1/4

A4 = area between y = x³ and the x-axis
integrating . . . I got 1/4

can't get all 4 of area 1/4

must have made a mistake somewhere.

 

[Gibbatron]

I got what Drongoski got. I think there must be a mistake with the question or we are missing some information, because the integral between y=1 and y=sqrt(x) is definitely 1/3, and you cant make it equal to 1/4. At least, i cant.

 

[ninetypercent]

Area of unit square of 1 x 1 cm = 1 cm^2

As y =x bisects the unit square,
The area between y = x and the x axis is 1 x 1 x 1/2 = 1/2 cm^2.
The area between the line y = 1 and y =x is therefore also 1/2 cm^2

Let the area between y =1 and y = x^3 be A
Let the area between y =x^3 and y = x be B
Let the area between y =x and y = root x be C
Let the area between y = root x and the x axis be D

Area under y = x^3


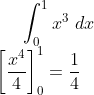Area C Area between y =x and y = rootx is equal to 1/2 - 1/4 = 1/4

but the area under y = x is equal to 1/2. and the area of C is equal to 1/4. therefore the area D is:
Area D 1/2 - 1/4 = 1/4

Area BThe area between y = x^3 and y = x


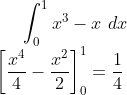Area A
(Area between y =1 and y =x) - Area B = 1/2 - 1/4 = 1/4

Since the area between all sub intervals is 1/4, the lines cut the unit square into 4 equal parts


EDIT: actually, I don't know. the above is incorrect