Area of unit square of 1 x 1 cm = 1 cm^2
As y =x bisects the unit square,
The area between y = x and the x axis is 1 x 1 x 1/2 = 1/2 cm^2.
The area between the line y = 1 and y =x is therefore also 1/2 cm^2
Let the area between y =1 and y = x^3 be A
Let the area between y =x^3 and y = x be B
Let the area between y =x and y = root x be C
Let the area between y = root x and the x axis be D
Area under y = x^3
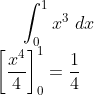 Area C
Area C Area between y =x and y = rootx is equal to 1/2 - 1/4 = 1/4
but the area under y = x is equal to 1/2. and the area of C is equal to 1/4. therefore the area D is:
Area D 1/2 - 1/4 = 1/4
Area BThe area between y = x^3 and y = x
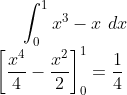 Area A
Area A
(Area between y =1 and y =x) - Area B = 1/2 - 1/4 = 1/4
Since the area between all sub intervals is 1/4, the lines cut the unit square into 4 equal parts
EDIT: actually, I don't know. the above is incorrect
