MetroMattums
Member
- Joined
- Apr 29, 2009
- Messages
- 231
- Gender
- Male
- HSC
- 2010
Can anyone evaluate:
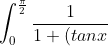^{k}} \,dx)
Thanks.
Thanks.
Let u=pi/2-x: du=-dxCan anyone evaluate:
Thanks.
Brilliant as always. By the way, shouldn't the f(a-x)dx in line 1 read f(b-x)dx ?
That's a very minor error. In the worst case scenario you could just write 'let a=b'...Brilliant as always. By the way, shouldn't the f(a-x)dx in line 1 read f(b-x)dx ?
