Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Official BOS Trial 2015 Thread (1 Viewer)
- Thread starter Carrotsticks
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
For (c) (ii), sketch y=(x^2-1)/(x^2+1) and y=kx+1, and you can see no matter what K value you pick (other than k=0, which cannot be the case anyway) you will always have exactly one point of intersection. In other words always one real root. From this, you can also see that when K is large, the real root approaches 0 (will be used later).does anyone know how to do question 15cii and iii?
For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.
Paradoxica
-insert title here-
Oh. Well I substituted four values, namely, -1/k, 1, 0 and -1For (c) (ii), sketch y=(x^2-1)/(x^2+1) and y=kx+1, and you can see no matter what K value you pick (other than k=0, which cannot be the case anyway) you will always have exactly one point of intersection. In other words always one real root. From this, you can also see that when K is large, the real root approaches 0 (will be used later).
For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.
P(-1/k) = 1-(1/k^2), P(1) = 2(k+1), P(0) = 2, P(-1) = 2(1-k)
We will now consider three cases for k.
Case 1: |k| < 1 means that P(-1/k) is negative. Combine with P(0) and there is a root by the intermediate value theorem.
Case 2: k < -1 means that P(1) is negative. Similar as above.
Case 3: k > 1 means that P(-1) is negative. Similar as above.
Degenerate cases occur if |k| = 1, as the root is trivial.
As you may have deduced already, I despise curve sketching.
Alternatively, can just differentiate P and show that its derivative has no zeros so P is monotonic (and use the fact that P has at least one real root, being a cubic (follows from IVT), so it has exactly one root)). Neither of these methods really use part (i) though, unless you subbed your values in to the expression in part (i), or differentiated the expression in part (i), but these are trivial ways to "use" it.Oh. Well I substituted four values, namely, -1/k, 1, 0 and -1
P(-1/k) = 1-(1/k^2), P(1) = 2(k+1), P(0) = 2, P(-1) = 2(1-k)
We will now consider three cases for k.
Case 1: |k| < 1 means that P(-1/k) is negative. Combine with P(0) and there is a root by the intermediate value theorem.
Case 2: k < -1 means that P(1) is negative. Similar as above.
Case 3: k > 1 means that P(-1) is negative. Similar as above.
Degenerate cases occur if |k| = 1, as the root is trivial.
As you may have deduced already, I despise curve sketching.
Paradoxica
-insert title here-
...OR you could just divide the entire cubic in it's reduced form by k, and letting k tend to infinity will degenerate the cubic into (x^2+1)x = 0For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Perhaps saying "Hence, or otherwise", would have been preferable.Alternatively, can just differentiate P and show that its derivative has no zeros so P is monotonic (and use the fact that P has at least one real root, being a cubic (follows from IVT), so it has exactly one root)). Neither of these methods really use part (i) though, unless you subbed your values in to the expression in part (i), or differentiated the expression in part (i), but these are trivial ways to "use" it.
This will find what the roots eventually become, but how would you then describe the behaviour of the roots as k varies? Part of the idea of the question was to get students to picture an 'animation' of what would happen to the roots as K gradually increases in value....OR you could just divide the entire cubic in it's reduced form by k, and letting k tend to infinity will degenerate the cubic into (x^2+1)x = 0
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Extension 1.Is this Extension 1 or 2?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
I admit Q12 was quite difficult.Extension 1.
However, I think Q14 is very reasonable.
Q14 (a) (i) can be done in two or three lines at most, with very little calculations (mostly explaining).
Q14 (a) (ii) is a little more difficult but it is implied that you simplify part (i) and take the sum of the simplified form.
It is unfamiliar though, you don't often see questions adding probabilities to prove binomial identities.
Q14 (b) and (c) are not difficult really (once you see the solution), but intimidating perhaps.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Theres no question 12 C ?
Was question 11d the result of newtons method of approximation ?
Was question 11d the result of newtons method of approximation ?
RealiseNothing
what is that?It is Cowpea
11d is pretty much the idea behind newtons method since you approximate roots using tangents.Theres no question 12 C ?
Was question 11d the result of newtons method of approximation ?
Paradoxica
-insert title here-
I rarely get intimidated. Frequently, however, I find myself flummoxed.Q14 (b) and (c) are not difficult really (once you see the solution), but intimidating perhaps.
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,755
- Gender
- Male
- HSC
- 2013
Did someone make origami during the papers lol? I spotted what looked like a crushed paper crane when cleaning at the end of the day.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
I was just scrolling.

I'm curious, what was the trap?
____________________
Hmm...Here's a question scrapped from 2U because it was too easy.
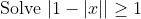
I'm curious, what was the trap?
____________________
Wait. How did you know what Q16 was gonna be before when you were in thereMy guesses are Simpsons rule/ trapezoidal rule or the AM-GM inequality
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
I think it would've been the fact that x=0 is a solution.I was just scrolling.
Hmm...
I'm curious, what was the trap?
____________________
Wait. How did you know what Q16 was gonna be before when you were in there
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Wait. How did you know what Q16 was gonna be before when you were in there
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Dunno, I made it pop out on it's own.I think it would've been the fact that x=0 is a solution.
________________________________
It's supposed to be my best topic. I haven't gone into beyond HSC yet but I had 98% of 4U integration in the bag sometime during Year 11 lolIf youre as good as you are in integration i reckon you could state rank
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Page 1 of question 16 was to prove AM-GM second was with trap rule lol...
