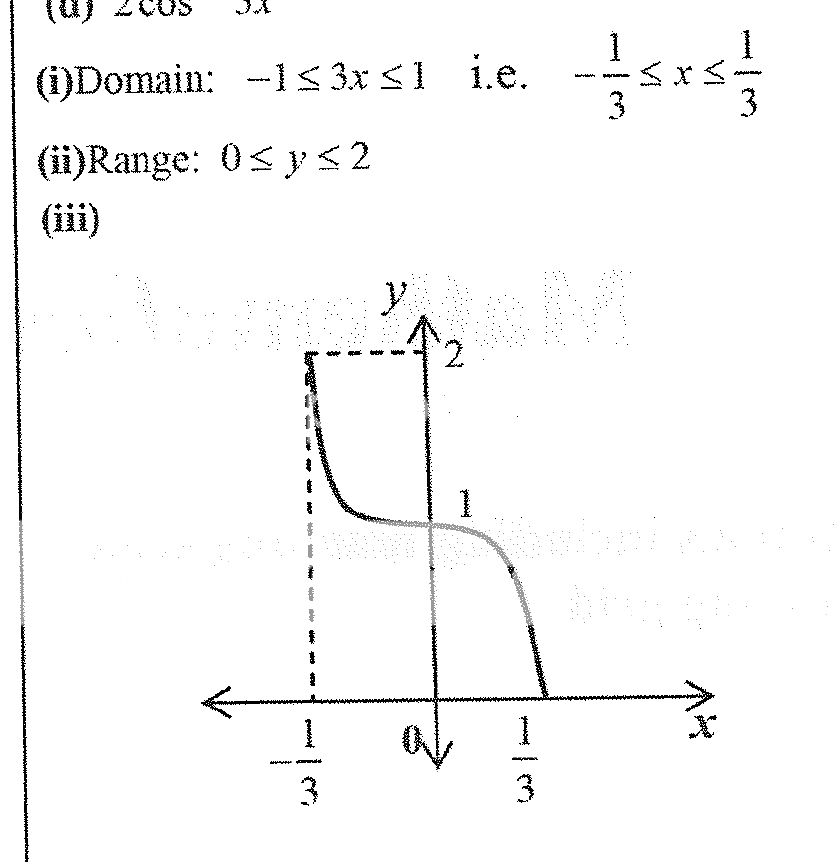
Re: HSC 2015 3U Marathon
could someone please explain this to me, last question from 2010 hsc
View attachment 32601
i] if you choose one ball, there are two possibilities, a red ball or a blue ball
if you choose two balls, there are three possibilities, 2 reds, 2 blues, or 1 red 1 blue
if you choose three balls, there are four possibilities, 3 reds, 3 blues, 2 red 1 blue, or two blue 1 red
following the pattern, choosing r balls, there are r+1 possibilities
ii] choosing (n-r) balls from n balls is nC(n-r) because groups of balls doesn't work on arrangements
using the rule, nC(n-r) = nCr we get the desired result
iii] the question asks n red balls and n blue balls (identical) and the labelled white balls
a selection of 'r' identical red and blue balls can be chosen in (r+1) ways, form part i]
therefore there are n-r white balls left, chosen in nCr ways part ii]
therefore selecting both can be made in (r+1) * nCr ways
the number of red or blue balls can go from 0 to n, so the total is sum from 0 to n [ (r+1) nCr ]
split that up into two different sums and use the answer from part b
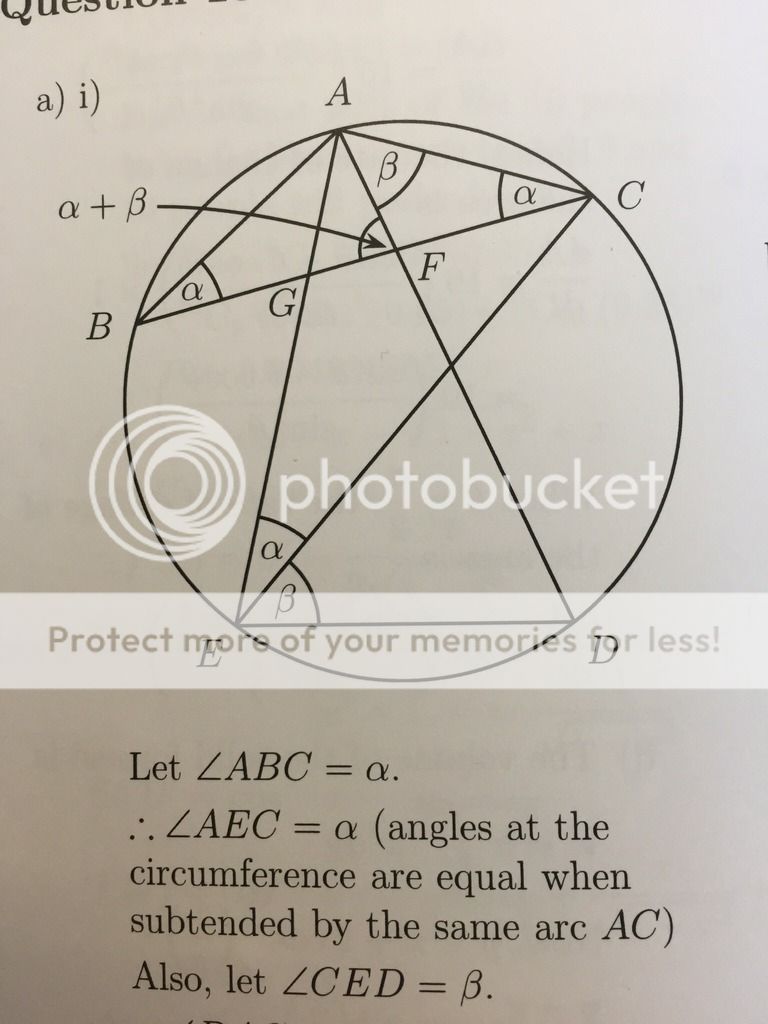
Would it be ok to say ' angles at the circumference are equal when subtended by the same chord AC' (insteading of saying the word arc'? (to express angle AEC and angle ABC)
Sometimes I see some solution say 'chord' or 'arc'.
Yes, arc or chord, same concept