I will probably have another think about it this evening to see if I can find a nicer way.
So I did have another think about it and couldn't come up with a much nicer way.
I wrote out my proof though, so perhaps that will be of some help to people who want to understand it more.
Remark: You might expect with an answer as simple as
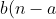(-1)^{a+b})
, there
must be a much quicker way of computing the sum. Whilst there could very well be a faster way of computing the sum, note that that expression is only valid under the assumption that a >= b. (If not, then think about the fact that each summand is symmetric in a and b, but the resulting sum is not!) If we wanted to relax the assumption that a >= b, our answer would actually be
\cdot(n-\max(a,b))\cdot (-1)^{a+b})
which is not quite as nice.
Also note that we had similar asymmetric dependence on the larger/smaller parameters in a trigonometric integral I posted in the MX2 integration marathon a while back, this behaviour crops up often when multiplying two oscillatory expressions that oscillate at different rates and then summing/integrating.
