-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (1 Viewer)
- Thread starter leehuan
- Start date
Paradoxica
-insert title here-
this feels like a memeI think you guys should enrol in Extreme Integration (MATH1052), or if you're feeling ambitious try Insane Integration (MATH3025)!
PM me for details.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
At least quick partial fractions is possible this time round lol
Really hope I'm right coz this took me forever. Also sorry for bad LaTeX.
+a^2)\mathrm{d}x)
+2a}{1+2a\mathrm{cos}(x)+a^2}\mathrm{d}x = \frac{1}{a}\int_0^{\pi} (1-\frac{1-a^2}{1+2a\mathrm{cos}(x)+a^2})\mathrm{d}x = \frac{\pi}{a}-\frac{1}{a}\int_0^{\pi} \frac{1-a^2}{1+2a\mathrm{cos}(x)+a^2})
+a^2}\mathrm{d}x)
Let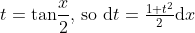
+a^2}\mathrm{d}x = \int_0^{\infty} \frac{1-a^2}{1+2a\frac{1-t^2}{1+t^2}+a^2}\frac{2}{1+t^2}\mathrm{d}t = 2\int_0^{\infty} \frac{1-a^2}{(1+2a+a^2)+(1-2a+a^2)t^2}\mathrm{d}t = 2\int_0^{\infty} \frac{(1-a)(1+a)}{(1+a)^2+(1-a)^2t^2}\mathrm{d}t = 2\int_0^{\infty} \frac{C}{C^2+t^2}\mathrm{d}t)
where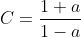
This is easily evaluated depending on the different cases:
If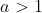 or
or 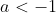 , we have
, we have 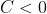
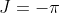 , if
, if 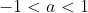 then
then 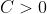 and
and 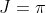 , and if
, and if 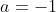 then
then 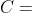 and
and 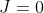 .
.
Case 1: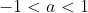
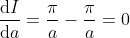 hence
hence 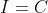 for some constant
for some constant 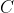 .
.
Evaluating the integral for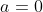 , we obtain that:
, we obtain that:
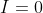 when
when 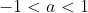 .
.
Case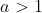 or
or 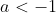 .
.
+a^2)\mathrm{d}x = \int_0^{\pi} \mathrm{ln}(1+2\frac{1}{a}\mathrm{cos}(x)+\frac{1}{a^2})\mathrm{d}x + \int_0^{\pi} 2\mathrm{ln}a\mathrm{d}x = 0 + 2\pi \mathrm{ln}(a)) (which follows from Case 1).
(which follows from Case 1).
) when
when 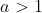 or
or 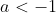 .
.
Case 3: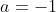
)\mathrm{d}x = \pi \mathrm{ln}2 + \int_0^{\pi} \mathrm{ln}(1-\mathrm{cos}(x))\mathrm{d}x)
Let)\mathrm{d}x)
By symmetry,)\mathrm{d}x+\int_0^{\frac{\pi}{2}} \mathrm{ln}(1+\mathrm{cos}(x))\mathrm{d}x=\int_0^{\frac{\pi}{2}} \mathrm{ln}(1-\mathrm{cos^2}(x))\mathrm{d}x=2\int_0^{\frac{\pi}{2}} \mathrm{ln}(\mathrm{sin}(x))\mathrm{d}x = 2\int_0^{\frac{\pi}{2}} \mathrm{ln}(\mathrm{cos}(x))\mathrm{d}x)
Let)\mathrm{d}x = \int_0^{\frac{\pi}{2}} \mathrm{ln}(\mathrm{sin}(x))\mathrm{d}x)
\mathrm{sin}(x))\mathrm{d}x = \int_0^{\frac{\pi}{2}} \mathrm{ln}(\frac{1}{2}\mathrm{sin}(2x))\mathrm{d}x = \int_0^{\frac{\pi}{2}} \mathrm{ln}(\frac{1}{2})\mathrm{d}x+\int_0^{\frac{\pi}{2}} \mathrm{ln}(\mathrm{sin}(2x))\mathrm{d}x + = \int_0^{\frac{\pi}{2}} \mathrm{ln}(\frac{1}{2})\mathrm{d}x+\frac{1}{2}\int_0^{\pi} \mathrm{ln}(\mathrm{sin}(u))\mathrm{d}u)
By symmetry,)\mathrm{d}u = 2\int_0^{\frac{\pi}{2}} \mathrm{ln}(\mathrm{sin}(u))\mathrm{d}u)
Therefore + L) , so
, so ) .
.
Subbing the values back in, we obtain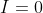 .
.
Case 4: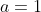
)\mathrm{d}x)
This can be done by the same method as case 3, and so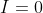 .
.
Hence, when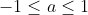 ,
, 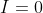 , and
, and ) otherwise.
otherwise.
Let
where
This is easily evaluated depending on the different cases:
If
Case 1:
Evaluating the integral for
Case
Case 3:
Let
By symmetry,
Let
By symmetry,
Therefore
Subbing the values back in, we obtain
Case 4:
This can be done by the same method as case 3, and so
Hence, when
Last edited:
Paradoxica
-insert title here-
Fourier ExpansionReally hope I'm right coz this took me forever. Also sorry for bad LaTeX.
No idea what that is, I'm not all that far beyond HSC mathsFourier Expansion
Paradoxica
-insert title here-
Bonus Challenge: Prove the last two integrals are symmetric in (a,b) <=> (b,a) without evaluating it to the final result.
Last edited:
Paradoxica
-insert title here-
For all positive real numbers, the iteration derived from Newton's Method applied to the equation q(x)=x²-2 results in the f(x) described above, and converges to the positive real root of the equation.
Shouldn't be hard assuming I didn't mess up typing the question.
Hence, fn(x) converges to √ ̅2 for x>0
The point x=0 can be discarded, as it is a set of zero measure.
Hence, the integral is equivalent to
My only problem with this question is that students don't know how to handle problematic points on the domain of an integral.
