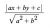SB257426
Very Important User
Im talking about this formula:
View attachment 40165
I was doing a hunters hill high extension 2 trial and they asked to find the min value of |z|. Would I need to derive this formula or can i just use it in an exam?
View attachment 40165
I was doing a hunters hill high extension 2 trial and they asked to find the min value of |z|. Would I need to derive this formula or can i just use it in an exam?