Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
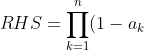 \\\\ = 1 - \sum_{k=1}^{n}a_k + \sum_{i<j}a_i a_j - ... + \prod_{k=1}^{n}a_k \\\\ > 1 - \sum_{k=1}^{n}a_k \\\\ = LHS )
haha.This is a question from our 4U test this afternoon (I hope I remembered it correctly...):
<a href="http://www.codecogs.com/eqnedit.php?latex=\textup{Prove by induction that }\\ (1-a_{1})(1-a_{2})...(1-a_{n})>1-(a_{1}@plus;a_{2}@plus;...@plus;a_{n})\\ \textup{for positive integers n}\geq 2 \textup{ where}\\ 0<a_{k}<1 \textup{ for }1<k<n" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\textup{Prove by induction that }\\ (1-a_{1})(1-a_{2})...(1-a_{n})>1-(a_{1}+a_{2}+...+a_{n})\\ \textup{for positive integers n}\geq 2 \textup{ where}\\ 0<a_{k}<1 \textup{ for }1<k<n" title="\textup{Prove by induction that }\\ (1-a_{1})(1-a_{2})...(1-a_{n})>1-(a_{1}+a_{2}+...+a_{n})\\ \textup{for positive integers n}\geq 2 \textup{ where}\\ 0<a_{k}<1 \textup{ for }1<k<n" /></a>
Last edited: