Maths complex number help (1 Viewer)

Run hard@thehsc · Nov 21, 2021

How do you do question 14?

notme123 · Nov 21, 2021

Run hard@thehsc said:
View attachment 34065
How do you do question 14?

you could turn this into a quadratic u^2 + Au + B where the constants are >0, and since the quadratic is positive definite (meaning its always above the x axis) that means it has no real roots. if x^2 has no real roots, neither can x.

Drongoski · Nov 21, 2021

Then P(x) will always be positive, i.e. cannot become zero. That means it cannot have real roots. That is you cannot find a real number "a" say, such that P(a) = 0.

To expand:
x^4 >= 0; Ax^2 >= 0; B > 0 ==> P(x) > 0
So the curve of y = P(x) cannot cross the x-axis; so no real roots !!!!!

Run hard@thehsc · Nov 21, 2021

@notme123 fair - are there other methods?

notme123 · Nov 21, 2021

Run hard@thehsc said:
@notme123 fair - are there other methods?

not on the top of my head rn

CM_Tutor · Nov 21, 2021

notme123 said:
you could turn this into a quadratic u^2 + Au + B where the constants are >0, and since the quadratic is positive definite (meaning its always above the x axis) that means it has no real roots. if x^2 has no real roots, neither can x.

Why is the quadratic positive definite?

notme123 · Nov 21, 2021

CM_Tutor said:
Why is the quadratic positive definite?

oh youre right thats not for certain lol.

notme123 · Nov 21, 2021

Run hard@thehsc said:
@notme123 fair - are there other methods?

oh i thought of another method. do the substitution as before where the roots are for x^2. now if you do sum of roots, the sum of the real parts would be -A which is less than 0. so if x^2 is less than 0, x must be not purely real

Trebla · Nov 21, 2021

Note that P'(x)=4x^3+2Ax and P''(x)=12x^2+2A.

P(x) is concave up with a minimum turning point at (0,B). Hence, P(x) > B > 0 so no real roots.

CM_Tutor · Nov 21, 2021

notme123 said:
oh i thought of another method. do the substitution as before where the roots are for x^2. now if you do sum of roots, the sum of the real parts would be -A which is less than 0. so if x^2 is less than 0, x must be not purely real

This requires the conjugate root theorem.

The result can be established without it, by proving that $x^2 < 0$ . This can be done by noting that

$x^2 = \cfrac{-A \pm \sqrt{\Delta}}{2} \qquad \text{where} \qquad \Delta = A^2 - 4B$

and that

$A,\ B \in \mathbb{R}^+\ \implies\ \Delta = A^2 - 4B < A^2\ \text{as}\ 4B > 0\ \implies\ \Delta < 0\ \text{or}\ 0 < \sqrt{\Delta} < A\ \text{as}\ A > 0$

$\text{If}\ \Delta < 0\ \text{then}\ x^2 \in \mathbb{C}\setminus\mathbb{R}\ \implies\ x \in \mathbb{C} \setminus \mathbb{R}$

$\text{If}\ 0 < \sqrt{\Delta} < A\ \text{then}\ x^2 = \cfrac{-A \pm \sqrt{\Delta}}{2}\ \implies\ -A < x^2 < 0\ \implies\ x \in \mathbb{C} \setminus \mathbb{R}$

Life'sHard · Nov 21, 2021

CM_Tutor said:
This requires the conjugate root theorem.

The result can be established without it, by proving that $x^2 < 0$ . This can be done by noting that

$x^2 = \cfrac{-A \pm \sqrt{\Delta}}{2} \qquad \text{where} \qquad \Delta = A^2 - 4B$

and that

$A,\ B \in \mathbb{R}^+\ \implies\ \Delta = A^2 - 4B < A^2\ \text{as}\ 4B > 0\ \implies\ \Delta < 0\ \text{or}\ 0 < \sqrt{\Delta} < A\ \text{as}\ A > 0$

$\text{If}\ \Delta < 0\ \text{then}\ x^2 \in \mathbb{C}\setminus\mathbb{R}\ \implies\ x \in \mathbb{C} \setminus \mathbb{R}$

$\text{If}\ 0 < \sqrt{\Delta} < A\ \text{then}\ x^2 = \cfrac{-A \pm \sqrt{\Delta}}{2}\ \implies\ -A < x^2 < 0\ \implies\ x \in \mathbb{C} \setminus \mathbb{R}$

Is latex broken? Or is it just me?

CM_Tutor · Nov 21, 2021

Life'sHard said:
Is latex broken? Or is it just me?

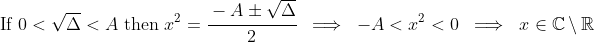
I've wondered the same... maybe @Trebla can explain?

Trebla · Nov 21, 2021

Yeah, looks like it is broken at the moment

5uckerberg · Nov 21, 2021

b is conjugate root theorem.

c is just the sum of 2 roots put together giving us

$A=c^{2}+d^{2}$ and $B=c^{2}d^{2}$ , $c^{4}+d^{4}=(c^{2}+d^{2})^{2}-2c^{2}d^{2}$ effectively just giving us $A^{2}-2B$

jimmysmith560 · Nov 22, 2021

It seems that LaTeX is currently experiencing some sort of issue that is preventing users from seeing particular input.

A temporary solution to this (if you're using a PC) is to right-click on the

icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).

The following message may appear:

This is due to the fact that the certificate for latex.codecogs.com has expired and needs to be updated. However, because the "Open image in new tab" option will only take you to an image file, there is most likely no real risk associated with proceeding, which can be done by clicking the "Advanced" button and then clicking on the "Proceed to latex.codecogs.com (unsafe)" option.

It is possible that the expired certificate of https://latex.codecogs.com/ is what is causing this issue.

Alternatively, you may wish to wait until https://latex.codecogs.com/ update their certificate, which will likely rectify the LaTeX issue on here.

Make a Difference – Donate to Bored of Studies!

Maths complex number help (1 Viewer)

Run hard@thehsc

Well-Known Member

notme123

Well-Known Member

Drongoski

Well-Known Member

Run hard@thehsc

Well-Known Member

notme123

Well-Known Member

CM_Tutor

Moderator

notme123

Well-Known Member

notme123

Well-Known Member

Trebla

Administrator

CM_Tutor

Moderator

Life'sHard

Well-Known Member

CM_Tutor

Moderator

Trebla

Administrator

5uckerberg

Well-Known Member

jimmysmith560

Le Phénix Trilingue

Users Who Are Viewing This Thread (Users: 0, Guests: 1)