Run hard@thehsc
Well-Known Member
- Joined
- Oct 7, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2022
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
you could turn this into a quadratic u^2 + Au + B where the constants are >0, and since the quadratic is positive definite (meaning its always above the x axis) that means it has no real roots. if x^2 has no real roots, neither can x.View attachment 34065
How do you do question 14?
not on the top of my head rn@notme123 fair - are there other methods?
Why is the quadratic positive definite?you could turn this into a quadratic u^2 + Au + B where the constants are >0, and since the quadratic is positive definite (meaning its always above the x axis) that means it has no real roots. if x^2 has no real roots, neither can x.
oh youre right thats not for certain lol.Why is the quadratic positive definite?
oh i thought of another method. do the substitution as before where the roots are for x^2. now if you do sum of roots, the sum of the real parts would be -A which is less than 0. so if x^2 is less than 0, x must be not purely real@notme123 fair - are there other methods?
This requires the conjugate root theorem.oh i thought of another method. do the substitution as before where the roots are for x^2. now if you do sum of roots, the sum of the real parts would be -A which is less than 0. so if x^2 is less than 0, x must be not purely real
Is latex broken? Or is it just me?This requires the conjugate root theorem.
The result can be established without it, by proving that. This can be done by noting that
and that
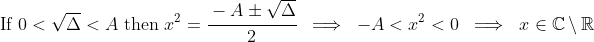
I've wondered the same... maybe @Trebla can explain?Is latex broken? Or is it just me?
 icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).
icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).