-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Quadratic question (1 Viewer)
- Thread starter sinophile
- Start date
hermand
je t'aime.
- Joined
- Aug 28, 2008
- Messages
- 1,432
- Gender
- Female
- HSC
- 2009
a.
find the gradient of the tangent, then normal.
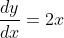
=4)

find the coordinates of point R.
when^{2}=4)
)
sub point and gradient into point-gradient formula.
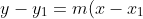)
)


b.
the normal cuts the parabola when it equals it.
change the previous answer into y-intercept form.





(x-2)=0)
since we already have x=2, we take
when ,
, ^{2})

)
find the gradient of the tangent, then normal.
find the coordinates of point R.
when
sub point and gradient into point-gradient formula.
b.
the normal cuts the parabola when it equals it.
change the previous answer into y-intercept form.
since we already have x=2, we take
when
x3.eddayyeeee
Member
- Joined
- Nov 4, 2008
- Messages
- 136
- Gender
- Male
- HSC
- 2011
a) First find the gradient of tangent to curve at x=2.
y=x^2 -> y'=2x.
sub x=2 into y'.
y'=4. So gradient is of tangent to curve at x= 2 is 4.
since normal is perpendicular to tangent, gradient of normal is -1/4 (ie. the negative recipricol)
y value of curve y=x^2 when x=2 is 4.
now.
use point gradient formuala. y-y,=m(x-x,) -> y - 4 = -1/4(x - 2)
rearranging that gives x+4y-18=0 as required.
b) simultaneous equations
y=x^2 (1)
x+4y-18=0 -> -x + 18 = 4y -> -x/4 + 18/4 =y (2)
equating equations
-x/4 + 18/4 = x^2
-x + 18 = 4x^2
4x^2 + x -18 = 0
(4x+9)(x-2) = 0
graphs intersect at x=2 & x= -9/4
since we already know about intersection @ x=2
find y value of normal when x= -9/4
then two numbers give the second point of intersection.
y=x^2 -> y'=2x.
sub x=2 into y'.
y'=4. So gradient is of tangent to curve at x= 2 is 4.
since normal is perpendicular to tangent, gradient of normal is -1/4 (ie. the negative recipricol)
y value of curve y=x^2 when x=2 is 4.
now.
use point gradient formuala. y-y,=m(x-x,) -> y - 4 = -1/4(x - 2)
rearranging that gives x+4y-18=0 as required.
b) simultaneous equations
y=x^2 (1)
x+4y-18=0 -> -x + 18 = 4y -> -x/4 + 18/4 =y (2)
equating equations
-x/4 + 18/4 = x^2
-x + 18 = 4x^2
4x^2 + x -18 = 0
(4x+9)(x-2) = 0
graphs intersect at x=2 & x= -9/4
since we already know about intersection @ x=2
find y value of normal when x= -9/4
then two numbers give the second point of intersection.
Timothy.Siu
Prophet 9
y'=2x, when x=2 y'=4a) Show that the equation of the normal to the curve y=x^2 at the point R where x=2 is given by x+4y-18=0
b) The normal intersects the parabola again at Q. Find the coordinates of Q.
therefore gradient of normal is -1/4
x=2, y=4
y-4=-1/4(x-2)
4y-16=-x+2
x+4y-18=0
y=(-x+18)/4
4x^2=-x+18
4x^2+x-18=0
x^2+x/4-9/2=0
we know x=2 is a factor, so the other one must be x=-9/4
x=-9/4 y=18/16
sinophile
Well-Known Member
- Joined
- Oct 25, 2008
- Messages
- 1,336
- Gender
- Undisclosed
- HSC
- N/A
Can you please explain to me how you factorised the equation?
Timothy.Siu
Prophet 9
grouped them and took x-2 as a factor and then factorisedCan you please explain to me how you factorised the equation?
4x^2-8x+9x-18=0
(x-2)4x+(x-2)9=0
(4x+9)(x-2)=0
hermand
je t'aime.
- Joined
- Aug 28, 2008
- Messages
- 1,432
- Gender
- Female
- HSC
- 2009
umm when i factorise quadratics when the x^2 has a coefficient greater than one, i use a grouping method.
multiply the y-intercept (numeral) by the coefficient of x, and find two multiples of the result that add to give the coefficient of x, and replace the x by these two multiples. then, take something common out of the first two terms, and something common out of the last two terms, ie, factorise the terms in pairs, and you should get a common value in the brackets. you then factorise the brackets out the front and end up with two sets of brackets, making the entire equation factorised.
ummmmm i'll give you all steps of example that explains it better than i can in words.


=-72)
=x)

+9(x-2)=0) [by factorising the (x-2) out of the equation.]
[by factorising the (x-2) out of the equation.]
(4x+9)=0)
multiply the y-intercept (numeral) by the coefficient of x, and find two multiples of the result that add to give the coefficient of x, and replace the x by these two multiples. then, take something common out of the first two terms, and something common out of the last two terms, ie, factorise the terms in pairs, and you should get a common value in the brackets. you then factorise the brackets out the front and end up with two sets of brackets, making the entire equation factorised.
ummmmm i'll give you all steps of example that explains it better than i can in words.
Another way to factorise a quadratic is to find its roots first.Can you please explain to me how you factorised the equation?
using the quadratic formula:
Now we have the roots we can "go backwards" to get the equation:
Now we multiply both sides by 4 to get rid of the fraction:
Just thought I'd mention this method because it always works and requires very little 'thinking'. You can always fall back to it in an exam when you're a bit frazzled.
eg you don't need to worry about doing stuff in your head, like "finding two multiples of the result that add to give the coefficient of x"
Timothy.Siu
Prophet 9
i rather complete the squareAnother way to factorise a quadratic is to find its roots first.
using the quadratic formula:
Now we have the roots we can "go backwards" to get the equation:
(I can do this because if I substitute x = 2 or -9/4 then LHS = RHS = 0 ie it is true)
(just tidying up brackets)
Now we multiply both sides by 4 to get rid of the fraction:
Just thought I'd mention this method because it always works and requires very little 'thinking'. You can always fall back to it in an exam when you're a bit frazzled.
eg you don't need to worry about doing stuff in your head, like "finding two multiples of the result that add to give the coefficient of x"
hermand
je t'aime.
- Joined
- Aug 28, 2008
- Messages
- 1,432
- Gender
- Female
- HSC
- 2009
isn't that a bit unnecessarily time consuming?Another way to factorise a quadratic is to find its roots first.
using the quadratic formula:
Now we have the roots we can "go backwards" to get the equation:
(I can do this because if I substitute x = 2 or -9/4 then LHS = RHS = 0 ie it is true)
(just tidying up brackets)
Now we multiply both sides by 4 to get rid of the fraction:
Just thought I'd mention this method because it always works and requires very little 'thinking'. You can always fall back to it in an exam when you're a bit frazzled.
eg you don't need to worry about doing stuff in your head, like "finding two multiples of the result that add to give the coefficient of x"
Not really... only takes 2 steps:isn't that a bit unnecessarily time consuming?
1) solve the quadratic, which shouldn't take more than a few seconds (giving x = a, b)
2) then write (x-a)(x-b) = 0
Timothy.Siu
Prophet 9
but u can just factorise it.Not really... only takes 2 steps:
1) solve the quadratic, which shouldn't take more than a few seconds (giving x = a, b)
2) then write (x-a)(x-b) = 0
hermand
je t'aime.
- Joined
- Aug 28, 2008
- Messages
- 1,432
- Gender
- Female
- HSC
- 2009
a few seconds? to write all that crap down and then use your calculator to find square roots etc? unlikely.Not really... only takes 2 steps:
1) solve the quadratic, which shouldn't take more than a few seconds (giving x = a, b)
2) then write (x-a)(x-b) = 0
and anyway, in exams, esp four unit, you want to conserve as much time as possible.
But you don't need "to write all that crap down", I just did so above to make it clear what I was doing.a few seconds? to write all that crap down and then use your calculator to find square roots etc? unlikely.
and anyway, in exams, esp four unit, you want to conserve as much time as possible.
I'm not saying you can't "just factorise" it, I was merely explaining another method that someone might find useful.
addikaye03
The A-Team
are you PSF ( product, sum, factorisation) people or cross method?? haha
im a PSF man. I rather completing the square though
im a PSF man. I rather completing the square though
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
To factor, i am a PSF person and sometimes a completing the squares person (pending on type of questionare you PSF ( product, sum, factorisation) people or cross method?? haha
im a PSF man. I rather completing the square though
