HSC 2013 MX2 Marathon (archive) (3 Viewers)

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

The way I did it was to use:

$\sum_{k=1}^{n} kcis(k\theta)$

Then equate imaginary parts to get the result:

$\frac{sin(n\theta) + nsin(\theta)[1-sin(n\theta)]}{2-2cos\theta} = \sum_{k=1}^{n} ksin(k\theta)$

Which is wrong, so idk.

Carrotsticks · Dec 27, 2012

Re: HSC 2013 4U Marathon

RealiseNothing said:
The way I did it was to use:

$\sum_{k=1}^{n} kcis(k\theta)$

Then equate imaginary parts to get the result:

$\frac{sin(n\theta) + nsin(\theta)[1-sin(n\theta)]}{2-2cos\theta} = \sum_{k=1}^{n} ksin(k\theta)$

Which is wrong, so idk.

Can you tell us how exactly you acquired

$\sum_{k=1}^{n} k cis (k\theta)$

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
Can you tell us how exactly you acquired

$\sum_{k=1}^{n} k cis (k\theta)$

$cis\theta + 2cis2\theta + 3cis3\theta + ... + ncisn\theta$

$cis\theta + 2cis^2\theta + 3cis^3\theta + ... + ncis^n\theta$ by De Moivre's Theorem

$(cis\theta + cis^2\theta + cis^3\theta + ...) + (cis^2\theta + cis^3\theta + ...) + (cis^3\theta + ...)$

Sum each one individually (a neat pattern arises). Then add them together and equate imaginary components.

Carrotsticks · Dec 27, 2012

Re: HSC 2013 4U Marathon

RealiseNothing said:
$cis\theta + 2cis2\theta + 3cis3\theta + ... + ncisn\theta$

$cis\theta + 2cis^2\theta + 3cis^3\theta + ... + ncis^n\theta$ by De Moivre's Theorem

$(cis\theta + cis^2\theta + cis^3\theta + ...) + (cis^2\theta + cis^3\theta + ...) + (cis^3\theta + ...)$

Sum each one individually (a neat pattern arises). Then add them together and equate imaginary components.

Yep, so quite like the first method I mentioned. That method SHOULD work, but there is much larger room for errors to be made. Try finding a closed form again, but using the second method I provided.

Sy123 · Dec 27, 2012

Re: HSC 2013 4U Marathon

$$Denote$ \ \ \ \ S_k(n) \equiv \sum_{r=0}^n r^k$

$$You may assume$ \ \ \ S_1(n)=\frac{n}{2}(n+1) \ \ \ \ \ S_2 (n) = \frac{n}{6}(n+1)(2n+1)$

$$i) By considering $ \sum_{r=0}^n (r+1)^k - r^k$

$$Show that$ \\ \\ kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{2}S_{k-2}(n) - \binom{k}{3}S_{k-3}(n) - ... - \binom{k}{k-1}S_1 (n)$

$ii) Hence, explain why$ \ \ S_k(n) \ \ $ is a polynomial of degree $ \ \ k+1 \ \ $ in $ \ \ n \ \ $ Show that this polynomial is divisible by n, and the sum of the coefficients is 1$

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

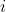$$i)$ \sum_{r=0}^{n}(r+1)^k - r^k = (n+1)^k$ by a telescoping sum.

Now expanding the binomial first instead of using a telescoping sum gives:

$(r+1)^k = \binom{k}{0} + \binom{k}{1}r + \binom{k}{2}r^2 + ... + \binom{k}{k}r^k$

Now if we apply the summation, we sum each one individually, that is:

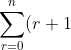$\sum_{r=0}^{n}(r+1)^k = \sum_{r=0}^{n}\binom{k}{0} + \sum_{r=0}^{n}\binom{k}{1}r + ... + \sum_{r=0}^{n}\binom{k}{k}r^k$

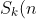Now using our definition of $S_k(n)$ we obtain:

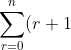$\sum_{r=0}^{n}(r+1)^k = (n+1) + \binom{k}{1}S_1(n) + \binom{k}{2}S_2(n) + ... + \binom{k}{k-1}S_{k-1}(n) + \binom{k}{k}S_k(n)$

Using the symmetry property of binomial expansions gives:

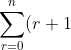$\sum_{r=0}^{n}(r+1)^k = (n+1) +\binom{k}{k-1}S_1(n) + \binom{k}{k-2}S_2(n) + ... + \binom{k}{1}S_{k-1}(n) + \binom{k}{0}S_k(n)$

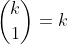
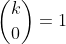
Now since $\binom{k}{1} = k$ and $\binom{k}{0} = 1$ we get:

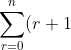$\sum_{r=0}^{n}(r+1)^k = (n+1) +\binom{k}{k-1}S_1(n) + \binom{k}{k-2}S_2(n) + ... + kS_{k-1}(n) + S_k(n)$

Now consider the second part of the equation:

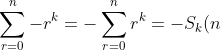$\sum_{r=0}^{n} -r^k = -\sum_{r=0}^{n} r^k = -S_k(n)$ by definition.

Hence if we add the two parts together we obtain:

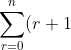$\sum_{r=0}^{n}(r+1)^k - r^k = (n+1) +\binom{k}{k-1}S_1(n) + \binom{k}{k-2}S_2(n) + ... + kS_{k-1}(n) + S_k(n) - S_k(n)$

So the two terms on the end cancel out and give:

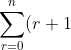$\sum_{r=0}^{n}(r+1)^k - r^k = (n+1) +\binom{k}{k-1}S_1(n) + \binom{k}{k-2}S_2(n) + ... + kS_{k-1}(n)$

But this was equal to the value of the telescoping sum, so we can equate the two and get:

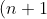$(n+1)^k = \sum_{r=0}^{n}(r+1)^k - r^k = (n+1) +\binom{k}{k-1}S_1(n) + \binom{k}{k-2}S_2(n) + ... + kS_{k-1}(n)$

Taking everything from the RHS to the LHS except for the last term gives us the required result of:

$kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{k-1}S_1(n) - \binom{k}{k-2}S_2(n) - ... - \binom{k}{2}S_{k-2}(n)$

Which can be re-written in the form asked:

$kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{2}S_{k-2}(n) - \binom{k}{3}S_{k-3}(n) - ... - \binom{k}{k-1}S_1(n)$

Quod Erat Demonstrandum.

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

I'll do part (ii) when my hands can be bothered latexing again lol.

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

How do I make it so that it is all on one line and doesn't go to the next?

Carrotsticks · Dec 27, 2012

Re: HSC 2013 4U Marathon

Don't think you can do that. It auto formats and goes into the next line when too long.

bleakarcher · Dec 27, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
Don't think you can do that. It auto formats and goes into the next line when too long.

Carrot, mind sharing some of the rejected BOS trial questions?

Carrotsticks · Dec 27, 2012

Re: HSC 2013 4U Marathon

bleakarcher said:
Carrot, mind sharing some of the rejected BOS trial questions?

2013 ones?

bleakarcher · Dec 27, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
2013 ones?

yeah, whichever ones you have to spare. I don't mind if it's a 2012 one.

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
$ii) Hence, explain why$ \ \ S_k(n) \ \ $ is a polynomial of degree $ \ \ k+1 \ \ $ in $ \ \ n \ \ $ Show that this polynomial is divisible by n, and the sum of the coefficients is 1$

Given:

$kS_{k-1}(n) = \sum_{r=0}^{n} kr^{k-1}$

Integrating the RHS gives:

$\sum_{r=0}^{n} r^k$

$=S_k(n)$

Therefore:

$\int kS_{k-1}(n) = S_k(n)$

Thus we can integrate the following to obtain $S_k(n)$ on the LHS:

$kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{2}S_{k-2}(n) - \binom{k}{3}S_{k-3}(n) - ... - \binom{k}{k-1}S_1 (n)$

Since the RHS is a polynomial in 'n' itself with highest degree 'k', it follows that after integration, the highest power will become 'k+1', and hence $S_k(n)$ is a polynomial of degree 'k+1' in 'n'.

bleakarcher · Dec 27, 2012

Re: HSC 2013 4U Marathon

RealiseNothing said:
Given:

$kS_{k-1}(n) = \sum_{r=0}^{n} kr^{k-1}$

Integrating the RHS gives:

$\sum_{r=0}^{n} r^k$

$=S_k(n)$

Therefore:

$\int kS_{k-1}(n) = S_k(n)$

Thus we can integrate the following to obtain $S_k(n)$ on the LHS:

$kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{2}S_{k-2}(n) - \binom{k}{3}S_{k-3}(n) - ... - \binom{k}{k-1}S_1 (n)$

Since the RHS is a polynomial in 'n' itself with highest degree 'k', it follows that after integration, the highest power will become 'k+1', and hence $S_k(n)$ is a polynomial of degree 'k+1' in 'n'.

You could have also replaced k with k+1.

RealiseNothing · Dec 27, 2012

Re: HSC 2013 4U Marathon

bleakarcher said:
You could have also replaced k with k+1.

lol that is so much easier.

Sy123 · Dec 27, 2012

Re: HSC 2013 4U Marathon

RealiseNothing said:
Given:

$kS_{k-1}(n) = \sum_{r=0}^{n} kr^{k-1}$

Integrating the RHS gives:

$\sum_{r=0}^{n} r^k$

$=S_k(n)$

Therefore:

$\int kS_{k-1}(n) = S_k(n)$

Thus we can integrate the following to obtain $S_k(n)$ on the LHS:

$kS_{k-1}(n) = (n+1)^k - (n+1) - \binom{k}{2}S_{k-2}(n) - \binom{k}{3}S_{k-3}(n) - ... - \binom{k}{k-1}S_1 (n)$

Since the RHS is a polynomial in 'n' itself with highest degree 'k', it follows that after integration, the highest power will become 'k+1', and hence $S_k(n)$ is a polynomial of degree 'k+1' in 'n'.

Nice work! Your approach to the first and second one was different to mine, I actually ripped this question off of STEP 2008 III Q2

Carrotsticks · Dec 27, 2012

Re: HSC 2013 4U Marathon

bleakarcher said:
yeah, whichever ones you have to spare. I don't mind if it's a 2012 one.

Not bothered atm to dig up the old BOS Trials thread, and can't find my spare question file for 2013 actually.

bleakarcher · Dec 27, 2012

Re: HSC 2013 4U Marathon

Carrotsticks said:
Not bothered atm to dig up the old BOS Trials thread, and can't find my spare question file for 2013 actually.

it's okay dude.

Sy123 · Dec 28, 2012

Re: HSC 2013 4U Marathon

I made this question just now:

$$If $ \ \ \ z= \cos \theta + i \sin \theta$

$$Consider $ \ \ \ (z+\frac{1}{z})^{2n}$

$$Show that$ \int_{0}^{\frac{\pi}{2}} \cos^{2n} \theta \ d\theta = \frac{\pi (2n)!}{2^{2n+1}(n!)^2}$

Carrotsticks · Dec 28, 2012

Re: HSC 2013 4U Marathon

Sy123 said:
I made this question just now:

$$If $ \ \ \ z= \cos \theta + i \sin \theta$

$$Consider $ \ \ \ (z+\frac{1}{z})^{2n}$

$$Show that$ \int_{0}^{\frac{\pi}{2}} \cos^{2n} \theta \ d\theta = \frac{\pi (2n)!}{2^{2n+1}(n!)^2}$

That feel when questions you made (legitimately) have already been asked in the HSC ='(

2009 Q7

HSC 2013 MX2 Marathon (archive) (3 Viewers)

what is that?It is Cowpea

Retired

what is that?It is Cowpea

Retired

This too shall pass

what is that?It is Cowpea

what is that?It is Cowpea

what is that?It is Cowpea

Retired

Active Member

Retired

Active Member

what is that?It is Cowpea

Active Member

what is that?It is Cowpea

This too shall pass

Retired

Active Member

This too shall pass

Retired

Users Who Are Viewing This Thread (Users: 0, Guests: 3)