Yes, you can blame me for that.this got serious real quick lol
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Can I get some help with questions? (1 Viewer)
- Thread starter jssicachoi
- Start date
Would this help?

Regarding this approach, the following formula is being used:

Alternatively, I suggest you refer to the following thread, where this specific question was covered in depth:
 boredofstudies.org
boredofstudies.org
I hope this helps!
Regarding this approach, the following formula is being used:
Alternatively, I suggest you refer to the following thread, where this specific question was covered in depth:
Is this part of our syllabus?
I hope this helps!
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
In the Venn diagram, the two circles are separated from one another and as such the union of the two cases is one probability added onto the other. Next, for mutually inclusive the idea is this inclusion-exclusion principle. That is clear,Wait so how does showing that m=n show their independent events?
View attachment 33612
Now, for our independent events what is the story there so basically what happens is that the events have no connection with one another so pretty much what happens is that if you want the two events together you multiply them. It is like oh a boy will be born from the mother's womb and it is also sunny out there. To be fair one can envision this as the two circles being separated situation. The way of attack after a bit of thought is this Independent or mutually exclusive circles in the Venn Diagram separate the circles, and mutually inclusive and dependent the circles in the Venn Diagram are together.
Think of it like this being excluded from a group is the harsh term for being independent of the group and included is when people are together and such. Just think of you and your friend folding arms looking in the opposite direction as mutually exclusive.
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Wait so how does showing that m=n show their independent events?
View attachment 33612
Attachments
-
159.9 KB Views: 11
Have you looked at my post here where I provided a different approach to this question?
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Yep, Cm_tutor's method explicitly shows what is going on but what I did is my interpretation. I sometimes feel bad not knowing but it is good to be able to learn a few things ourselves.
Last edited:
So you would end up with geometric series = num_minutes_in_a_year, where n= num_times_finger_snapped. There is no way to solve this numerically so you will need to use inspection
The official solution is as follows:
This question also requires a knowledge of logarithms. Don’t stress if you don’t understand it yet!
To solve a problem like this, it is often helpful to draw a diagram and/or table to illustrate what is happening. It then becomes easier to spot a pattern. We will draw a table to compare the number of finger snaps (n) with the total time elapsed in minutes (t):
Can we find some mathematical expression that will give us the time elapsed for a certain number of finger snaps? Since the time elapsed between finger snaps always doubles, we would expect powers of 2 to be involved in the expression. In fact, we notice that the numbers in the time elapsed column are all 1 less than a power of 2. We could try the expression
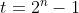
but this doesn’t quite work. With a little bit of thought, you should realise that
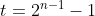
is the correct expression. Since we can now calculate the time elapsed for any given number of finger snaps, we can work out how many finger snaps fit into a year. We do this by first finding the number of minutes in a year.
We could of course look this up on the internet; but we really should be able to work it out for ourselves! One year is 365 days, which is 365 × 24 hours, i.e. 8760 hours. This in turn is 8760 × 60 minutes; so there are 525600 minutes in a year.
Now we ask the question: for which value of n (for how many finger snaps) do we get a value of t that is close to the number of minutes in a year? In other words, we want to solve , which gives
, which gives
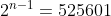
)
}{\:\log _{10}\left(2\right)}+1)
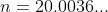
Since we can only have a whole number of finger snaps, we have shown that by following the pattern, we would only snap our fingers 20 times in one year.
I hope this helps!
This question also requires a knowledge of logarithms. Don’t stress if you don’t understand it yet!
To solve a problem like this, it is often helpful to draw a diagram and/or table to illustrate what is happening. It then becomes easier to spot a pattern. We will draw a table to compare the number of finger snaps (n) with the total time elapsed in minutes (t):
Can we find some mathematical expression that will give us the time elapsed for a certain number of finger snaps? Since the time elapsed between finger snaps always doubles, we would expect powers of 2 to be involved in the expression. In fact, we notice that the numbers in the time elapsed column are all 1 less than a power of 2. We could try the expression
We could of course look this up on the internet; but we really should be able to work it out for ourselves! One year is 365 days, which is 365 × 24 hours, i.e. 8760 hours. This in turn is 8760 × 60 minutes; so there are 525600 minutes in a year.
Now we ask the question: for which value of n (for how many finger snaps) do we get a value of t that is close to the number of minutes in a year? In other words, we want to solve
Since we can only have a whole number of finger snaps, we have shown that by following the pattern, we would only snap our fingers 20 times in one year.
I hope this helps!
- Joined
- Feb 26, 2008
- Messages
- 5,310
- Gender
- Male
- HSC
- 2011
This one is a similar problem: https://www.gocomics.com/foxtrot/2006/09/10
In all cases, for the percentage change, we use the formula:Hivaclibtibcharkwa said:
b) For men, percentage increase =
For women, percentage increase =
c) Percentage increase =
d) In shops, percentage increase =
In pubs, percentage change =
I hope this helps!
So x is the current amount of lemonade as a fraction which may be less than one. You are taking 1/3 of current amount of lemonade not the full jug.View attachment 35247
Seems simple enough right? The answer the university gave is 1/3 + 1/2 = 5/6
But i wrote an equation for it and got a different answer being 3/4
View attachment 35248
To explain the equation.
x is the amount of lemonade in the jug to start off with.
1/3 of x was sold and then only one half of the jug was left
Am i doing something wrong? or is the question wrong?
Pretty much cossine's advice, solving this question algebraically would be as follows:
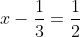
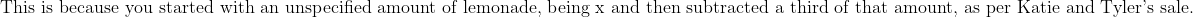
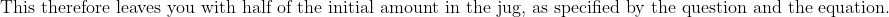
Solving the equation will allow us to find the required fraction:

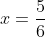 ,
, 
I hope this helps!
Solving the equation will allow us to find the required fraction:
I hope this helps!
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 338
- Gender
- Male
- HSC
- 2022
Put more simply;
Any lemonade at the start of the day has either been sold or remains in the jug. Now the question says 1/3 of a jug (no particular relation to the initial amount) was sold, and 1/2 of a jug remains. So the lemonade at the start is 1/3 + 1/2 = 5/6. Interpret the values as proprotions of a jug, not relations to the initial or final amounts.
Any lemonade at the start of the day has either been sold or remains in the jug. Now the question says 1/3 of a jug (no particular relation to the initial amount) was sold, and 1/2 of a jug remains. So the lemonade at the start is 1/3 + 1/2 = 5/6. Interpret the values as proprotions of a jug, not relations to the initial or final amounts.
In addition to the above, and in order to confirm the original answer, there is a slight variant of this question from the University of Wollongong, where the only difference is that the numbers were swapped (which leads to the same answer), as follows:Your assuming that x = 1. That's the only way you know that 1/3 of x is really 1/3
Eg. If the jug was 5/6 then one-third of the jug would be 5/18 not 1/3
In your example if the jug was 1 then 1/3 of 1 is 1/3. Hence you can do the subtraction. But we don't know that which is why we go
x (being the unknown amount in the jug) - (1/3 * x) being 1/3 of the unknown amount. View attachment 35251
Katie and Tyler are working at their lemonade stand. They have sold
The solution to the above version of the question is as follows:
To find out how much lemonade they started with, we can add how much they sold to how much they have left:
Therefore, Katie and Tyler started with
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Wait @Hivaclibtibcharkwa which uni course is this and which uni is this from?
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
It has to be UWS. Right?
First, perform the necessary conversions:
- To go from g to kg, we divide the mass value by 1000. This means that 8.9g is 0.0089kg
- To go from
to
, we multiply the volume value by 1000. This means that
In scientific notation, this would be expressed as
I hope this helps!
The null hypothesis is always an equality. The reason for this is computation.Can someone help me with these question, like with question b would the null hypothesis be that it’s less than 70 or would the alternative hypothesis say that?
Because the definition p-value is
p-value = P(getting test statistic that is more contradictory or equally contradictory to the null hypothesis | H0 )
It may help to read Probability and Statistics for Engineering Sciences by Jay L. Devore
It will explain things in more detail
So give the question a go first and I will check the working out.Ah sorry just realised I didn’t put in the imahe
In this case
H0: mean_weight = 70
Ha: mean_weight <= 70.



