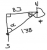
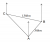
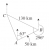
In general, we reject the null hypothesis if the p-value is less than the significance level α.
If the alternative hypothesis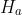 contains the not‐equal‐to symbol (≠), the hypothesis test is a two‐tailed test. Otherwise, all other tests are one-tailed.
contains the not‐equal‐to symbol (≠), the hypothesis test is a two‐tailed test. Otherwise, all other tests are one-tailed.
If needed, below are solutions to each part, based on the above information. As cossine mentioned, definitely try to attempt the question(s) first to see if you can apply your understanding in your working:
Part (a):
Suppose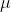 is the average age of Sydney residents; then
is the average age of Sydney residents; then 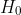 is
is 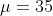 , and
, and 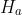 is
is 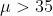 . Note that this is a one-tailed hypothesis test. Here, the p-value 0.0170 is less than the significance level
. Note that this is a one-tailed hypothesis test. Here, the p-value 0.0170 is less than the significance level 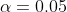 . So we reject the null hypothesis.
. So we reject the null hypothesis.
Conclusion: this sample information does indicate that the mean age in Sydney has increased from 35 years.
Part (b):
Let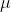 be the average weight of this population; then
be the average weight of this population; then 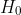 is
is 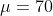 , and
, and 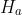 is
is 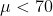 . This is a one-tailed test. The standard deviation of weights in this population is
. This is a one-tailed test. The standard deviation of weights in this population is 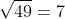 . Here, the p-value 0.001 is less than the significance level
. Here, the p-value 0.001 is less than the significance level 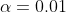 . So we reject the null hypothesis.
. So we reject the null hypothesis.
Conclusion: the sample data do provide enough evidence for us to conclude that the mean weight for the population is less than 70 kg.
Part (c):
Let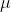 be the average IQ score of this population; then
be the average IQ score of this population; then 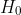 is
is 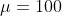 , and
, and 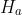 is
is 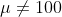 . This is a two-tailed test. Here, the p-value 0.095 is greater than the significance level
. This is a two-tailed test. Here, the p-value 0.095 is greater than the significance level 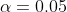 . So we do not reject the null hypothesis.
. So we do not reject the null hypothesis.
Conclusion: on the basis of these data, we cannot conclude that the mean IQ score for this population is not 100.
I hope this helps!
If the alternative hypothesis
If needed, below are solutions to each part, based on the above information. As cossine mentioned, definitely try to attempt the question(s) first to see if you can apply your understanding in your working:
Part (a):
Suppose
Conclusion: this sample information does indicate that the mean age in Sydney has increased from 35 years.
Part (b):
Let
Conclusion: the sample data do provide enough evidence for us to conclude that the mean weight for the population is less than 70 kg.
Part (c):
Let
Conclusion: on the basis of these data, we cannot conclude that the mean IQ score for this population is not 100.
I hope this helps!